2.1.a Twelve equal charges, \(q\), are situated at the corners of a regular 12-sided polygon (for instance, one on each numeral of a clock face). What is the net force on a test Charge \(Q\) at the centre?

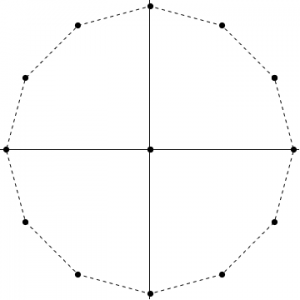
In order to find the net force on \(Q\) apply the principle of superposition and sum the forces acting on \(Q\). The model for the net force on \(Q\) is

\begin{equation}
\vec{F}_{Q} = \sum_{n=1}^{12} \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{n \pi}{6} \right) \, \hat{i} + \sin \left( \frac{n \pi}{6} \right) \, \hat{j} \right)
\end{equation}

By symmetry each nth radial contains two charges \(q\) which results in zero net force. For example,

$$\frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{n \pi}{6} \right) \, \hat{i} + \sin \left( \frac{n \pi}{6} \right) \, \hat{j} \right) + \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{ (n+6) \pi}{6} \right) \, \hat{i} + \sin \left( \frac{(n+6) \pi}{6} \right) \, \hat{j} \right) = \vec{0}$$

$$\frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left[ \left( \cos \left( \frac{n \pi}{6} \right) + \cos \left( \frac{n \pi}{6} + \pi \right) \right) \, \hat{i} + \left( \sin \left( \frac{n \pi}{6} \right) + \sin \left( \frac{n \pi}{6} + \pi \right) \right) \, \hat{j} \right] = \vec{0}$$

Summing the six radials yields \(\vec{F}_Q = \vec{0} \).

2.1.b Suppose one of the 12 \(q\)’s is removed. What is the force on \(Q\)?

Due to symmetry considering the answer when a particular charge is deleted does not create a loss of generality. Deleting the last charge

$$\vec{F}_{Q} = \sum_{n=1}^{11} \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{n \pi}{6} \right) \, \hat{i} + \sin \left( \frac{n \pi}{6} \right) \, \hat{j} \right)$$

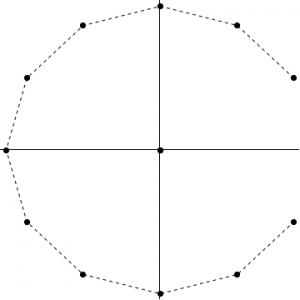
Under this arrangement all the charges are “balanced” except the \(q\) at \( (-R, 0) \). Therefore,

$$\vec{F}_Q = \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \hat{i}$$

In general the force will be parallel to the radial containing the deleted charge.

Also note that by exploiting the pairwise symmetry the computation can be simplified. The next problem demonstrates how the lack of pairwise symmetric makes the computation a bit more tedious.

2.1.c Now 13 equal charges, \(q\), are placed at the corners of a regular 13-sided polygon. What is the force on a test charge \(Q\) at the centre?

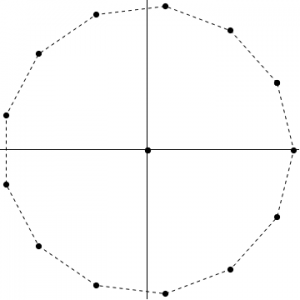
Again the goal is to apply the principle of superposition and to sum the forces acting on \(\vec{F}_Q\). The model is

\begin{equation}
\vec{F}_{Q} = \sum_{n=1}^{13} \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{2 n \pi}{13} \right) \, \hat{i} + \sin \left( \frac{2 n \pi}{13} \right) \, \hat{j} \right)
\end{equation}

First consider the sum of the forces in \(\hat{i}\) . This amounts to computing \(\sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) \), which is

$$\cos \left(\frac{2 \pi }{13}\right) + \cos \left(\frac{4 \pi }{13}\right)+ \cos \left(\frac{6 \pi }{13}\right)+\cos \left(\frac{8\pi }{13}\right)+ \cos \left(\frac{10 \pi }{13}\right)+ \cos \left(\frac{12 \pi }{13}\right) + \cos \left(\frac{14 \pi }{13}\right) + \cdots$$

$$ \cdots + \cos \left(\frac{16 \pi }{13}\right)+ \cos \left(\frac{18 \pi }{13}\right)+\cos \left(\frac{20\pi }{13}\right)+ \cos \left(\frac{22 \pi }{13}\right)+ \cos \left(\frac{24 \pi }{13}\right) + 1$$

We will use the following identities to compute \(\sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) \).

Equation 1

\begin{equation}
\cos \beta + \cos ( \beta + \alpha) + \cos ( \beta + 2 \alpha) + \cdots + \cos ( \beta + n \alpha) = \frac{ \sin \left( \frac{(n+1) \alpha}{2} \right) \cdot \cos \left( \beta + \frac{n \alpha}{2}\right) }{\sin \frac{\alpha}{2}}
\end{equation}

Equation 2

\begin{equation}
\sum_{n=1}^{N} \cos (n \theta) = – \frac{1}{2} + \frac{\sin \left( N + \frac{1}{2} \right) \theta}{ 2 \sin \left( \frac{\theta}{2}\right)}
\end{equation}

First apply (1) by letting \( \beta=0 \) and \( \alpha = \frac{2 \pi}{13}\)

$$\cos(0) + \cos \left( 0 + \frac{2 \pi}{13} \right) + \cos \left( 0 + 2 \frac{2 \pi}{13} \right) + \cdots + \cos \left( 0 + 13 \frac{2 \pi}{13}\right) = \frac{\sin \left(\frac{(13+1) (\frac{2 \pi}{13} )}{2}\right) \cdot \cos \left(0+\frac{13 (\frac{2 \pi}{13} )}{2} \right)}{\sin \left(\frac{ \frac{2 \pi}{13} }{2}\right)}$$

$$1 + \sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) = \frac{\sin( \pi) \cos \left( \frac{\pi}{13} \right) + \sin \left( \frac{\pi}{13} \right) \cos( \pi)}{ \sin \left(\frac{\pi }{13}\right)} = 1$$

$$\sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) = 0$$

Second, applying (2) yields

$$\sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) = -\frac{1}{2}+\frac{\sin \left( \left(13+\frac{1}{2}\right) \frac{2 \pi }{13}\right)}{2 \sin \left(\frac{\pi }{13}\right)}$$

$$\sum_{n=1}^{13} \cos \left( \frac{2 n \pi}{13} \right) = -\frac{1}{2}+\frac{\sin \left( \left(13+\frac{1}{2}\right) \frac{2 \pi }{13}\right)}{2 \sin \left(\frac{\pi }{13}\right)} = -\frac{1}{2} +\frac{\sin( 2 \pi) \cos \left( \frac{\pi}{13} \right) + \sin \left( \frac{\pi}{13} \right) \cos( 2 \pi)}{2 \sin \left(\frac{\pi }{13}\right)} =0$$

You may have been attempted to apply the cofunction identity which yields

$$\cos \left(\frac{2 \pi }{13}\right)+\sin \left(\frac{5 \pi }{26}\right)+\sin \left(\frac{\pi }{26}\right)-\sin \left(\frac{3 \pi }{26}\right)-\cos \left(\frac{3 \pi }{13}\right)-\cos \left(\frac{\pi }{13}\right)-\cos \left(\frac{\pi }{13}\right) \cdots$$

$$ \cdots -\cos \left(\frac{3 \pi }{13}\right)-\sin \left(\frac{3 \pi }{26}\right)-\sin \left(\frac{\pi }{26}\right)+\sin \left(\frac{5 \pi }{26}\right)+\cos \left(\frac{2 \pi }{13}\right)+1$$

which simplifies to

$$1 -2 \sin \left(\frac{\pi }{26}\right)-2 \sin \left(\frac{3 \pi }{26}\right)+2 \sin \left(\frac{5 \pi }{26}\right)-2 \cos \left(\frac{\pi }{13}\right)+2 \cos \left(\frac{2 \pi }{13}\right)-2 \cos \left(\frac{3 \pi }{13}\right)$$

This answer is equal to zero but it is not obvious, in my opinion; however, interestingly enough, applying the cofunction identity to the \(\hat{j}\) components does sum neatly to zero.

$$\sum_{n=1}^{13} \sin \left( \frac{2 n \pi}{13} \right) = \sin \left(\frac{2 \pi }{13}\right)+\cos \left(\frac{5 \pi }{26}\right)+\cos \left(\frac{\pi }{26}\right)+\cos \left(\frac{3 \pi }{26}\right)+\sin \left(\frac{3 \pi }{13}\right)+\sin \left(\frac{\pi }{13}\right) + \cdots$$

$$\cdots -\sin \left(\frac{\pi }{13}\right)-\sin \left(\frac{3 \pi }{13}\right)-\cos \left(\frac{3 \pi }{26}\right)-\cos \left(\frac{\pi }{26}\right)-\cos \left(\frac{5 \pi }{26}\right)-\sin \left(\frac{2 \pi }{13}\right) + 0 = 0$$

What does this imply about the geometry?

Generalizing the Previous Results

The previous two results suggest that it is possible to derive a general formula that demonstrates the net force on a test charge located at the centre of a regular polygonal configuration of \(m\) charges, \(q\), is zero.

\begin{equation}
\vec{F}_{Q} = \sum_{n=1}^{m} \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{2 n \pi}{m} \right) \, \hat{i} + \sin \left( \frac{2 n \pi}{m} \right) \, \hat{j} \right)
\end{equation}

Again consider the components independently and show that each sum is zero. Applying Lagrange’s identities to each case as appropriate yields

$$\sum_{n=1}^{m} \cos \left( \frac{2 n \pi}{m} \right) = -\frac{1}{2}+\frac{\sin \left( \left(m+\frac{1}{2}\right) \frac{2 \pi }{m}\right)}{2 \sin \left(\frac{\pi }{m}\right)} = -\frac{1}{2} +\frac{\sin( 2 \pi) \cos \left( \frac{\pi}{m} \right) + \sin \left( \frac{\pi}{m} \right) \cos( 2 \pi)}{2 \sin \left(\frac{\pi }{m}\right)} =0$$

similarly using the appropriate Lagrange identity for sine

$$\sum_{n=1}^{m} \sin \left( \frac{2 n \pi}{m} \right) = \frac{1}{2} \cot \left( \frac{\pi}{m} \right)-\frac{\cos \left( \left(m+\frac{1}{2}\right) \frac{2 \pi }{m}\right)}{2 \sin \left(\frac{\pi }{m}\right)} = \frac{\cos \left( \frac{\pi}{m} \right)}{2\sin \left( \frac{\pi}{m} \right)} – \frac{\cos( 2 \pi) \cos \left( \frac{\pi}{m} \right) – \sin \left( \frac{\pi}{m} \right) \sin( 2 \pi)}{2 \sin \left(\frac{\pi }{m}\right)} =0$$

2.1.d If one of the 13 \(q\)’s is removed, what is the force on \(Q\)?

$$\vec{F}_{Q} = \sum_{n=1}^{12} \frac{1}{4 \pi \epsilon_0} \frac{qQ}{R^2} \left( \cos \left( \frac{2 n \pi}{13} \right) \, \hat{i} + \sin \left( \frac{2 n \pi}{13} \right) \, \hat{j} \right)$$