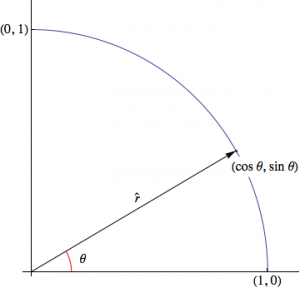
Referring to the diagram above the polar unit vector \( \hat{ r } \) has the following relation to the rectangular unit vectors \( \hat{ i } \) and \( \hat{ j } \)

$$ \hat{r} = \left(\cos \theta \right) \hat{i} + \left( \sin \theta \right ) \hat{j} $$

 

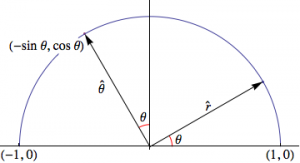
The polar unit vector \( \hat{ \theta } \) is always perpendicular to \( \hat{ r } \). From the diagram above \( \hat{ \theta } \) has the following relation to the rectangular unit vectors \( \hat{ i } \) and \( \hat{ j } \)

$$ \hat{ \theta} = \left( -\sin \theta \right) \hat{i} + \left( \cos \theta \right) \hat{j} $$

 

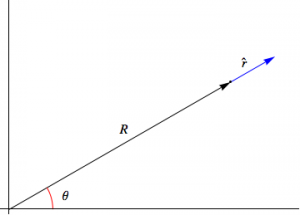
In polar coordinates the position of an object \( R \) distance from the origin as represented in the diagram above is modelled
$$ \mathbf{r} = R \hat{r} $$

The velocity and acceleration in polar coordinates is derived by differentiating the position vector.

$$ \frac{ d \mathbf{r}}{dt} = \frac { d R }{dt} \hat{r} + R \frac{ d \hat{r}}{dt} $$

Differentiating \( \hat{ r } \) yields

$$ \frac{d \hat{r}}{dt} = \left(-\frac{d \theta}{dt} \sin \theta \right) \hat{i} + \left( \frac{d \theta}{dt} \cos \theta \right ) \hat{j} = \frac{d \theta}{dt} \left[ \left( -\sin \theta \right) \hat{i} + \left( \cos \theta \right) \hat{j} \right] $$
$$ \frac{d \hat{r}}{dt} = \frac{d \theta}{dt} \hat{ \theta} $$

which implies the velocity is

$$ \frac{ d \mathbf{r}}{dt} = \frac { d R }{dt} \hat{r} + R \frac{d \theta}{dt} \hat{ \theta} $$

Differentiating the velocity yields acceleration.

$$ \frac{d^2 \mathbf{r}}{dt^2} = \frac{ d^2 R}{dt^2} \hat{r} + \frac{dR}{dt} \frac{d \hat{r}}{dt} + \left( \frac{dR}{dt}\frac{d \theta}{dt} + R \frac{ d^2 \theta}{dt^2} \right) \hat{ \theta} + R \frac{ d \theta}{dt} \frac{ d \hat{ \theta}}{dt} $$

differentiating \( \hat{ \theta } \)

$$ \frac{d \hat{ \theta}}{dt} = \left(-\frac{d \theta}{dt} \cos \theta \right) \hat{i} + \left( – \frac{d \theta}{dt} \sin \theta \right ) \hat{j} = -\frac{d \theta}{dt} \left[ \left( \cos \theta \right) \hat{i} + \left( \sin \theta \right) \hat{j} \right] $$
$$ \frac{d \hat{ \theta}}{dt} = -\frac{d \theta}{dt} \hat{r} $$

substituting appropriately yields

$$ \frac{d^2 \mathbf{r}}{dt^2} = \frac{ d^2 R}{dt^2} \hat{r} + \left( \frac{dR}{dt}\frac{d \theta}{dt} + R \frac{ d^2 \theta}{dt^2} \right) \hat{ \theta} + \frac{dR}{dt} \frac{d \theta}{dt} \hat{ \theta} – R \left( \frac{ d \theta}{dt} \right)^2 \hat{r} $$

or

$$\frac{d^2 \mathbf{r}}{dt^2} = \left( \frac{ d^2 R}{dt^2} – R \left( \frac{ d \theta}{dt} \right)^2 \right) \hat{r} + \left( 2\frac{dR}{dt} \frac{d \theta}{dt} – R \frac{ d^2 \theta}{dt^2} \right) \hat{ \theta} $$